Unit 5 - Descriptives (pt. 2)

PSYC 640 - Fall 2024

Dustin Haraden, PhD

Reminders

  • Journal Entries

  • Lab 1 - Now due 10/6

Last Class

  • Focused on basic descriptives
    • mean()
    • median()
    • describe()

Today…

Explore correlations and comparing means.

# File management
library(here)
# for dplyr, ggplot2
library(tidyverse)
# Loading data
library(rio)
# Pretty tables
library(sjPlot)
library(kableExtra)
# Putting Plots together
library(patchwork)

#Remove Scientific Notation 
options(scipen=999)

Import cleaned up file

Last class we created a new .csv file named named_Sleep_Data. We will continue to use that! Let’s make sure to import that data.

# Remember that your path will probably be different
sleep_data <- read.csv(here("lectures", 
                            "data", 
                            "named_Sleep_Data.csv"))

Relationships between variables

Association - Correlation

Examine the relationship between two continuous variables

Similar to the mean and standard deviation, but it is between two variables

Typically displayed as a scatterplot

Code 
set.seed(42)

n <- 200
x <- rnorm(n, mean = 10, sd = 2)
y <- 2 * x + rnorm(n, mean = 0, sd = 2) 
corr_data <- data.frame(x,y)

corr_data %>% 
  ggplot(aes(x,y)) + 
  geom_point() + 
  geom_smooth(method="lm", 
              se = FALSE) + 
  labs(
    x = "Number of Houses", 
    y = "Amount of Candy"
  )

Association - Covariance

Before we talk about correlation, we need to take a look at covariance

\[ cov_{xy} = \frac{\sum(x-\bar{x})(y-\bar{y})}{N-1} \]

  • Covariance can be thought of as the “average cross product” between two variables

  • It captures the raw/unstandardized relationship between two variables

  • Covariance matrix is the basis for many statistical analyses

Covariance to Correlation

The Pearson correlation coefficient \(r\) addresses this by standardizing the covariance

It is done in the same way that we would create a \(z-score\)…by dividing by the standard deviation

\[ r_{xy} = \frac{Cov(x,y)}{sd_x sd_y} \]

Correlations

  • Tells us: How much 2 variables are linearly related

  • Range: -1 to +1

  • Most common and basic effect size measure

  • Is used to build the regression model

Interpreting Correlations (5.7.5)

Correlation Strength Direction
-1.0 to -0.9 Very Strong Negative
-0.9 to -0.7 Strong Negative
-0.7 to -0.4 Moderate Negative
-0.4 to -0.2 Weak Negative
-0.2 to 0 Negligible Negative
0 to 0.2 Negligible Positive
0.2 to 0.4 Weak Positive
0.4 to 0.7 Moderate Positive
0.7 to 0.9 Strong Positive
0.9 to 1.0 Very Strong Positive

Pearson Correlations in R

Calculating Correlation in R

Now how do we get a correlation value in R?

cor(corr_data$x, corr_data$y)
[1] 0.8929946

That will give us the correlation, but we also want to know how to get our p-value

Correlation Test

To get the test of a single pair of variables, we will use the cor.test() function:

cor.test(x, y, data = corr_data)

    Pearson's product-moment correlation

data:  x and y
t = 27.919, df = 198, p-value < 0.00000000000000022
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.8609168 0.9180000
sample estimates:
      cor 
0.8929946

Using real data - Epworth Sleepiness Scale

So far we have been looking at single variables, but we often care about the relationships between multiple variables in a dataset

Code 
sleep_data %>% 
  select(ESS1m1:ESS8m1) %>% 
  cor() %>% 
  kable()
ESS1m1 ESS2m1 ESS3m1 ESS4m1 ESS5m1 ESS6m1 ESS7m1 ESS8m1
ESS1m1 1 NA NA NA NA NA NA NA
ESS2m1 NA 1 NA NA NA NA NA NA
ESS3m1 NA NA 1 NA NA NA NA NA
ESS4m1 NA NA NA 1 NA NA NA NA
ESS5m1 NA NA NA NA 1 NA NA NA
ESS6m1 NA NA NA NA NA 1 NA NA
ESS7m1 NA NA NA NA NA NA 1 NA
ESS8m1 NA NA NA NA NA NA NA 1

Missing Values - na.rm = TRUE?

Handling Missing - Correlation

  • Listwise Deletion (complete cases)

    • Removes participants completely if they are missing a value being compared
    • Smaller Sample Sizes
    • Doesn’t bias correlation estimate

  • Pairwise Deletion

    • Removes participants for that single pair, but leaves information in when there are complete information
    • Larger Sample Sizes
    • Could bias estimates if there is a systematic reason things are missing
sleep_data %>% 
  select(ESS1m1:ESS8m1) %>% 
  cor(use = "complete") %>% 
  kable()
ESS1m1 ESS2m1 ESS3m1 ESS4m1 ESS5m1 ESS6m1 ESS7m1 ESS8m1
ESS1m1 1.0000000 0.3303236 0.2784836 0.1455593 0.2295289 0.1422071 0.2206383 0.0984444
ESS2m1 0.3303236 1.0000000 0.1976108 0.1387409 0.2190331 0.1748049 0.2134999 0.1010883
ESS3m1 0.2784836 0.1976108 1.0000000 0.2920448 0.1948408 0.2888370 0.2778982 0.2178073
ESS4m1 0.1455593 0.1387409 0.2920448 1.0000000 0.2579808 0.0897873 0.2589136 0.2409171
ESS5m1 0.2295289 0.2190331 0.1948408 0.2579808 1.0000000 0.0704590 0.2821851 0.0629151
ESS6m1 0.1422071 0.1748049 0.2888370 0.0897873 0.0704590 1.0000000 0.2833070 0.3493524
ESS7m1 0.2206383 0.2134999 0.2778982 0.2589136 0.2821851 0.2833070 1.0000000 0.2356524
ESS8m1 0.0984444 0.1010883 0.2178073 0.2409171 0.0629151 0.3493524 0.2356524 1.0000000 
sleep_data %>% 
  select(ESS1m1:ESS8m1) %>% 
  cor(use = "pairwise") %>% 
  kable()
ESS1m1 ESS2m1 ESS3m1 ESS4m1 ESS5m1 ESS6m1 ESS7m1 ESS8m1
ESS1m1 1.0000000 0.3303236 0.2784836 0.1455593 0.2295289 0.1422071 0.2206383 0.0984444
ESS2m1 0.3303236 1.0000000 0.1976108 0.1387409 0.2190331 0.1748049 0.2134999 0.1010883
ESS3m1 0.2784836 0.1976108 1.0000000 0.2920448 0.1948408 0.2888370 0.2778982 0.2178073
ESS4m1 0.1455593 0.1387409 0.2920448 1.0000000 0.2579808 0.0897873 0.2589136 0.2409171
ESS5m1 0.2295289 0.2190331 0.1948408 0.2579808 1.0000000 0.0704590 0.2821851 0.0629151
ESS6m1 0.1422071 0.1748049 0.2888370 0.0897873 0.0704590 1.0000000 0.2833070 0.3493524
ESS7m1 0.2206383 0.2134999 0.2778982 0.2589136 0.2821851 0.2833070 1.0000000 0.2356524
ESS8m1 0.0984444 0.1010883 0.2178073 0.2409171 0.0629151 0.3493524 0.2356524 1.0000000

Spearman’s Rank Correaltion

Spearman’s Rank Correlation

We need to be able to capture this different (ordinal) “relationship”

  • If student 1 works more hours than student 2, then we can guarantee that student 1 will get a better grade

Instead of using the amount given by the variables (“hours studied”), we rank the variables based on least (rank = 1) to most (rank = 10)

Then we correlate the rankings with one another

Foundations of Statistics

Who were those white dudes that started this?

Statistics and Eugenics

The concept of the correlation is primarily attributed to Sir Frances Galton

The correlation coefficient was developed by his student, Karl Pearson, and adapted into the ANOVA framework by Sir Ronald Fisher

  • Both were prominent advocates for the eugenics movement

What do we do with this info?

Be aware of the assumptions

  • Statistics are often thought of as being absent of bias…they are just numbers

  • Statistical significance was a way to avoid talking about nuance or degree.

  • “Correlation does not imply causation” was a refutation of work demonstrating associations between environment and poverty.

  • Need to be particularly mindful of our goals as scientists and how they can influence the way we interpret the findings

Fancy Tables

Correlation Tables

Before we used the cor() function to create a correlation matrix of our variables

But what is missing?

sleep_data %>% 
  select(ESS1m1:ESS8m1) %>% 
  cor(use = "complete") %>% 
  kable()
ESS1m1 ESS2m1 ESS3m1 ESS4m1 ESS5m1 ESS6m1 ESS7m1 ESS8m1
ESS1m1 1.0000000 0.3303236 0.2784836 0.1455593 0.2295289 0.1422071 0.2206383 0.0984444
ESS2m1 0.3303236 1.0000000 0.1976108 0.1387409 0.2190331 0.1748049 0.2134999 0.1010883
ESS3m1 0.2784836 0.1976108 1.0000000 0.2920448 0.1948408 0.2888370 0.2778982 0.2178073
ESS4m1 0.1455593 0.1387409 0.2920448 1.0000000 0.2579808 0.0897873 0.2589136 0.2409171
ESS5m1 0.2295289 0.2190331 0.1948408 0.2579808 1.0000000 0.0704590 0.2821851 0.0629151
ESS6m1 0.1422071 0.1748049 0.2888370 0.0897873 0.0704590 1.0000000 0.2833070 0.3493524
ESS7m1 0.2206383 0.2134999 0.2778982 0.2589136 0.2821851 0.2833070 1.0000000 0.2356524
ESS8m1 0.0984444 0.1010883 0.2178073 0.2409171 0.0629151 0.3493524 0.2356524 1.0000000

Correlation Tables - sjPlot

sleep_data %>% 
  select(ESS1m1:ESS8m1) %>% 
  cor(use = "complete") %>% 
  tab_corr(na.deletion = "listwise", triangle = "lower")
  ESS1m1 ESS2m1 ESS3m1 ESS4m1 ESS5m1 ESS6m1 ESS7m1 ESS8m1
ESS1m1                
ESS2m1 0.330              
ESS3m1 0.278 0.198            
ESS4m1 0.146 0.139 0.292          
ESS5m1 0.230 0.219 0.195 0.258        
ESS6m1 0.142 0.175 0.289 0.090 0.070      
ESS7m1 0.221 0.213 0.278 0.259 0.282 0.283    
ESS8m1 0.098 0.101 0.218 0.241 0.063 0.349 0.236  
Computed correlation used pearson-method with listwise-deletion.

Correlation Tables - sjPlot

So many different cusomizations for this type of plot

Can add titles, indicate what missingness and method

Saves you a TON of time when putting it into a manuscript

Writing up a Correlation

Template: r(degress of freedom) = the r statistic, p = p value.

Imagine we have conducted a study of 40 students that looked at whether IQ scores and GPA are correlated. We might report the results like this:

IQ and GPA were found to be moderately positively correlated, r(38) = .34, p = .032.

Other example:

Among the students of Hogwarts University, the number of hours playing Fortnite per week and midterm exam results were negatively correlated, r(78) = -.45, p < .001.

And another:

Table 1 reports descriptive statistics and correlations among variables of interest. Knowledge of Weird Al Songs was positively correlated with perceptions of humor for Dr. Haraden (r(49) = .79, p <.001), such that the more Weird Al songs a student knew, the more they thought Dr. Haraden was funny.

Visualizing Data

Visualizing Data

It is always important to visualize our data! Even after getting the correlations and other descriptives

Let’s look at some data:

Code 
data1 <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/data1.csv") %>% 
  mutate(dataset = "data1")

data2 <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/data2.csv") %>% 
  mutate(dataset = "data2")

data3 <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/data3.csv") %>% 
  mutate(dataset = "data3")

And then combine them to make it easier to do summary stats

three_data <- bind_rows(data1, data2, data3)

Descriptive Stats on the 3 datasets

three_data %>%
  group_by(dataset) %>% 
  summarize(
    mean_x = mean(x),
    mean_y = mean(y),
    std_x = sd(x), 
    std_y = sd(y), 
    cor_xy = cor(x,y)
  )
# A tibble: 3 × 6
  dataset mean_x mean_y std_x std_y  cor_xy
  <chr>    <dbl>  <dbl> <dbl> <dbl>   <dbl>
1 data1     54.3   47.8  16.8  26.9 -0.0641
2 data2     54.3   47.8  16.8  26.9 -0.0683
3 data3     54.3   47.8  16.8  26.9 -0.0645

Visualizing Dataset 1

Code 
data1 %>% 
  ggplot(aes(x, y)) + 
  geom_point() + 
  labs(title = "Dataset 1")

Visualizing Dataset 1

Code 
vis1 <- data1 %>% 
  ggplot(aes(x, y)) + 
  geom_point() + 
  labs(title = "Dataset 1") +
  geom_smooth(method = "lm", 
              se = FALSE)
vis1

Visualizing Dataset 2

Code 
vis2 <- data2 %>% 
  ggplot(aes(x, y)) + 
  geom_point() + 
  labs(title = "Dataset 2") +
  geom_smooth(method = "lm", 
              se = FALSE)
vis2

Finally…Dataset 3

Code 
vis3 <- data3 %>% 
  ggplot(aes(x, y)) + 
  geom_point() + 
  labs(title = "Dataset 3") +
  geom_smooth(method = "lm", 
              se = FALSE)
vis3

Not all data are created equally

vis1 + vis2 + vis3

ALWAYS VISUALIZE YOUR DATA

Comparing Means

Comparing Means

Calculated using a t-test. To calculate the t-statistic, you will use this formula:

\[t_{df=N-1} = \frac{\bar{X}-\mu}{\frac{\hat{\sigma}}{\sqrt{N}}}\]

The heavier tails of the t-distribution, especially for small N, are the penalty we pay for having to estimate the population standard deviation from the sample.

Types of t-Tests

Single Samples t-test

Independent Samples t-test

Paired Samples t-test

Dataset

Moving forward for today, we will use this dataset

  • 100 students from New York

  • 100 students from New Mexico

state_school <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/NM-NY_CAS.csv")

Normality Assumption

  1. Check for Normality: Visualizing data (histograms), Q-Q plots, and statistical tests (Shapiro-Wilk, Anderson-Darling) to assess normality.

  2. Remedies for Violations: data transformation or non-parametric alternatives when data is not normally distributed.

Independent Samples t-test

Two different types: Student’s & Welch’s

  • Start with Student’s t-test which assumes equal variances between the groups

\[ t = \frac{\bar{X_1} - \bar{X_2}}{SE(\bar{X_1} - \bar{X_2})} \]

Student’s t-test

\[ H_0 : \mu_1 = \mu_2 \ \ H_1 : \mu_1 \neq \mu_2 \]

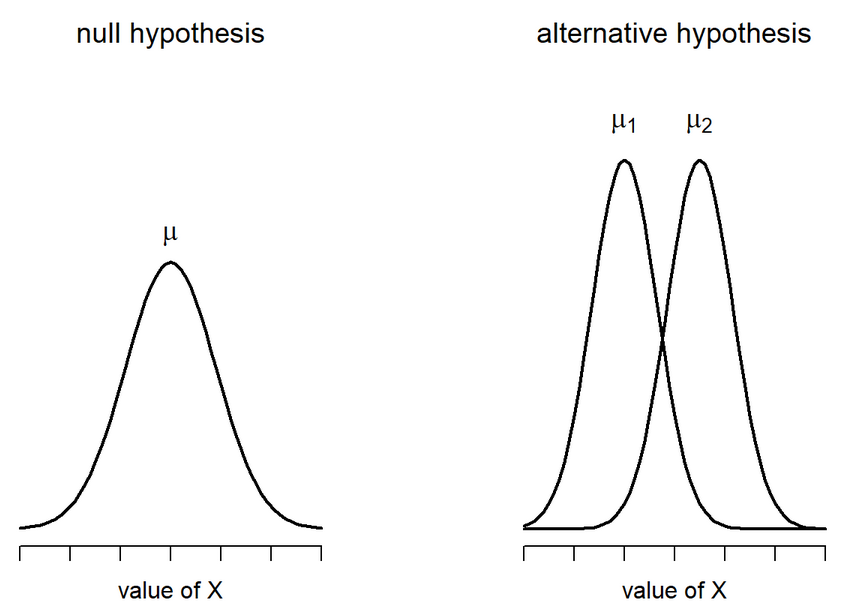
Student’s t-test: Calculate SE

Are able to use a pooled variance estimate

Both variances/standard deviations are assumed to be equal

Therefore:

\[ SE(\bar{X_1} - \bar{X_2}) = \hat{\sigma} \sqrt{\frac{1}{N_1} + \frac{1}{N_2}} \]

We are calculating the Standard Error of the Difference between means

Degrees of Freedom: Total N - 2

Student’s t-test

Let’s try it out using the traditional t.test() function

t.test(
  formula = Sleep_Hours_Schoolnight ~ Region, 
  data = state_school, 
  var.equal = TRUE
)

    Two Sample t-test

data:  Sleep_Hours_Schoolnight by Region
t = -0.023951, df = 180, p-value = 0.9809
alternative hypothesis: true difference in means between group NM and group NY is not equal to 0
95 percent confidence interval:
 -0.4281648  0.4178954
sample estimates:
mean in group NM mean in group NY 
        6.989247         6.994382

Student’s t-test: Write-up

The mean amount of sleep in New Mexico for youth was 6.989 (SD = 1.379), while the mean in New York was 6.994 (SD = 1.512). A Student’s independent samples t-test showed that there was not a significant mean difference (t(180)=-0.024, p=.981, \(CI_{95}\)=[-0.43, 0.42], d=.004). This suggests that there is no difference between youth in NM and NY on amount of sleep on school nights.

Welch’s t-test

\[ H_0 : \mu_1 = \mu_2 \ \ H_1 : \mu_1 \neq \mu_2 \]

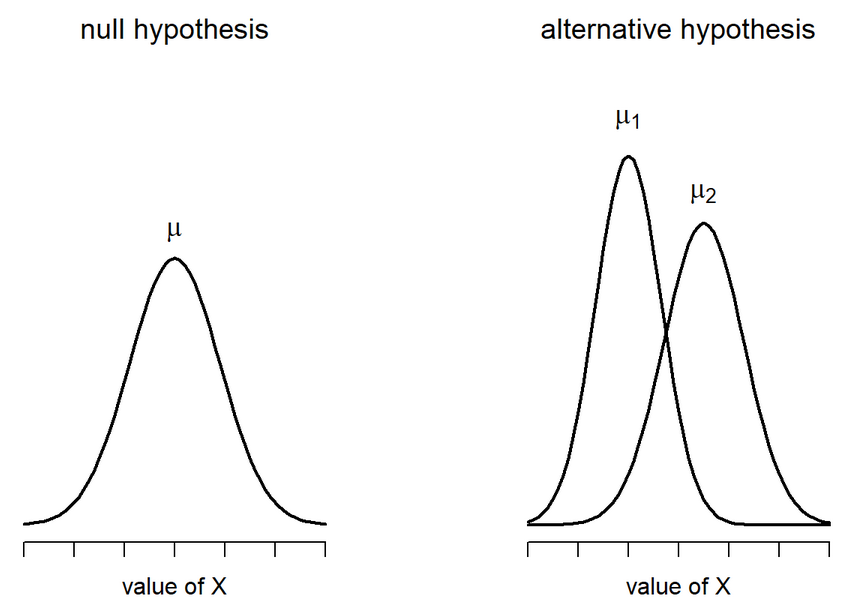
Welch’s t-test: Calculate SE

Since the variances are not equal, we have to estimate the SE differently

\[ SE(\bar{X_1} - \bar{X_2}) = \sqrt{\frac{\hat{\sigma_1^2}}{N_1} + \frac{\hat{\sigma_2^2}}{N_2}} \]

Degrees of Freedom is also very different:

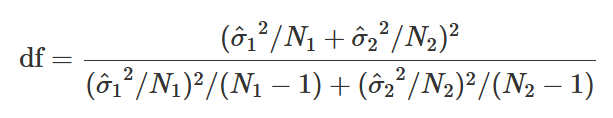
Welch’s t-test: In R (classic)

Let’s try it out using the traditional t.test() function…turns out it is pretty straightforward

t.test(
  formula = Sleep_Hours_Schoolnight ~ Region, 
  data = state_school, 
  var.equal = FALSE
)

    Welch Two Sample t-test

data:  Sleep_Hours_Schoolnight by Region
t = -0.023902, df = 176.74, p-value = 0.981
alternative hypothesis: true difference in means between group NM and group NY is not equal to 0
95 percent confidence interval:
 -0.4290776  0.4188082
sample estimates:
mean in group NM mean in group NY 
        6.989247         6.994382

Cool Visualizations

The library ggstatsplot has some wonderful visualizations of various tests

Code 
ggstatsplot::ggbetweenstats(
  data  = state_school,
  x     = Region,
  y     = Sleep_Hours_Schoolnight,
  title = "Distribution of hours of sleep across Region"
)