Week 03: Describe & Vizualize
Date: September 8, 2025
Today

Starting Up
Let’s first start by opening our Project
Then, create a new Notebook/Markdown Document that we will use for today
Setup the libraries and bring in the data
- We will use the TIPI data from the last lecture that has already been scored
Descriptive Statistics
How old is Dr. Haraden?
Some Terminology
| Population | Sample |
|---|---|
| \(\mu\) (mu) = Population Mean | \(\bar{X}\) (x bar) = Sample Mean |
| \(\sigma\) (sigma) = Population Standard Deviation | \(s\) = \(\hat{\sigma}\) = Sample Standard Deviation |
| \(\sigma^2\) (sigma squared) = Population Variance | \(s^2\) = \(\hat{\sigma^2}\) = Sample Variance |
Measures of Central Tendency
For a given set of observations, measures of central tendency allow us to get the “gist” of the data.
They tell us about where the “average” or the “mid-point” of the data lies or how much deviation there is from a central point.
Let’s take a look at the data that we have already loaded in, and complete some of these tasks.
Mean/Average
\[ \bar{X} = \frac{X_1+X_2+...+X\_{N-1}X_N}{N} \]
OR
\[ \bar{X} = \frac{1}{N}\sum_{i=1}^{N} X_i \]
Mean in R
A quick way to find the mean is to use the aptly named mean() function from base R. Use this function to get the average age and ess total in our dataset.
A mean of NA makes no sense…
Sometimes we forgot to account for the missing variables in our variable! We got NA! The reason for this is that the mean is calculated by using every value for a given variable, so if you don’t remove (or impute) the missing values before getting the mean, it won’t work.
Here is how you would account for that:
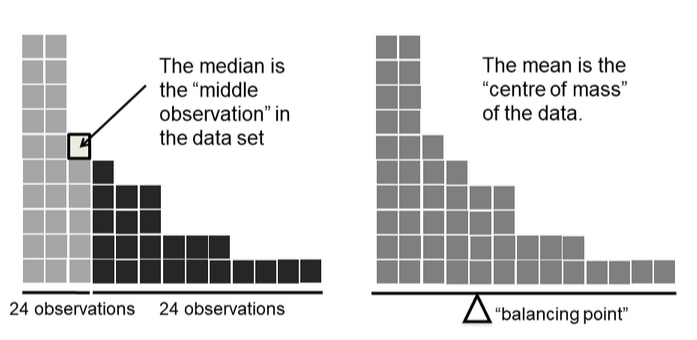
Median
The median is the middle value of a set of observations: 50% of the data points fall below the median, and 50% fall above.
To find the median, we can use the median() function. Use it on the age variable.
Measures of Variability
The overall spread of the data; How far from the middle?
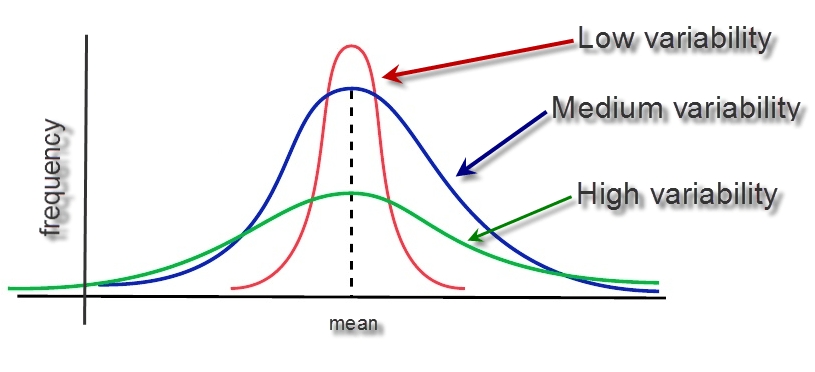
Range
The range gives us the distance between the smallest and largest value in a dataset.
You can find the range using the range() function, which will output the minimum and maximum values.
Find the range of the duration_in_seconds variable.
Variance and Standard Deviation
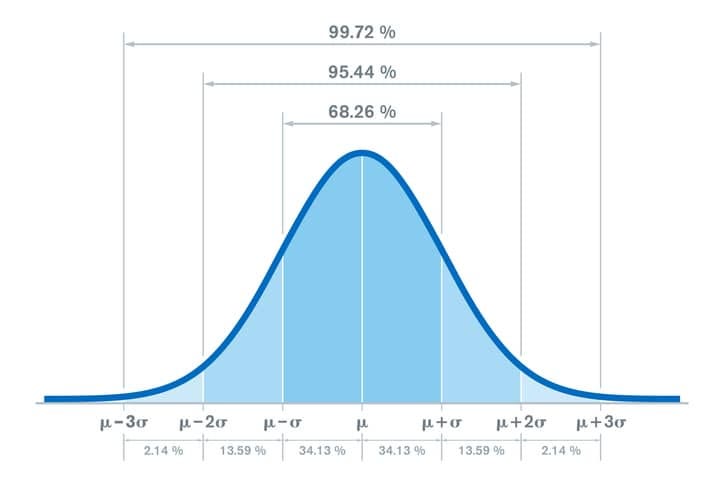
68-95-99.7 Rule
For nearly normally distributed data:
about 68% falls within 1 SD of the mean,
about 95% falls within 2 SD of the mean,
about 99.7% falls within 3 SD of the mean.
It is possible for observations to fall 4, 5, or more standard deviations away from the mean, but these occurrences are very rare if the data are nearly normal.
Variance
The sum of squared deviations
\[\sigma^2 = \frac{1}{N}\sum_{i=1}^N(X-\bar{X})^2\]
\[\hat{\sigma}^2 = s^2 = \frac{1}{N-1}\sum_{i=1}^N(X-\bar{X})^2\]
| \(i\) (observation) | \(X_i\) (value) | \(\bar{X}\) (sample mean) | \(X_i - \bar{X}\) (deviation from mean) | \((X_i - \bar{X})^2\) (squared deviation) |
|---|---|---|---|---|
| 1 | 56 | 36.6 | 19.4 | 376.36 |
| 2 | 31 | 36.6 | -5.6 | 31.36 |
| 3 | 56 | 36.6 | 19.4 | 376.36 |
| 4 | 8 | 36.6 | -28.6 | 817.96 |
| 5 | 32 | 36.6 | -4.6 | 21.16 |
Why do we use the squared deviation in the calculation of variance?
To get rid of negative values so that observations equally distant from the mean are weighted equally
To weigh larger deviations from the mean
In-Class Activity: Variance
Open up Instagram (that is still a thing right?)
Identify a celebrity and look at their most recent Instagram posts.
Let’s calculate the variance of their likes.

Variance in R
To find the variance and standard deviation, we use var() and sd(), respectively. Find the variance and standard deviation of the age variable.
Summarizing Data
So far we have been calculating various descriptive statistics (somewhat painstakingly) using an assortment of different functions. So what if we have a dataset with a bunch of variables we want descriptive statistics for? Surely we don’t want to calculate descriptives for each variable by hand…
Fortunately for us, there is a function called describe() from the {psych} package, which we can use to quickly summarize a whole set of variables in a dataset.
Be sure to first install the package prior to putting it into your library code chunk. Reminder: anytime you add a library, be sure you actually run the code line library(psych). Otherwise, you will have a hard time trying to use the next functions.
Let’s use it with our sleep dataset!
describe()
This function automatically calculates all of the descriptives we reviewed above (and more!). Use the describe() function from the psych package on the entire sleep_data dataset.
Notes: If you load a library at the beginning, you can directly call any function from it. Instead, you can call a function by library_name::function_name without loading the entire library.
vars n mean sd median trimmed mad min
id 1 99 1058.12 31.05 1059.0 1057.93 38.55 1006.0
progress 2 99 100.00 0.00 100.0 100.00 0.00 100.0
duration_in_seconds 3 99 7197.29 34904.64 1461.0 1527.88 486.29 623.0
consent 4 99 1.00 0.00 1.0 1.00 0.00 1.0
genderid 5 99 4.46 0.82 4.0 4.47 1.48 1.0
genderid_7_text* 6 99 1.03 0.22 1.0 1.00 0.00 1.0
sex 7 99 1.51 0.50 2.0 1.51 0.00 1.0
age 8 99 19.78 1.84 20.0 19.53 1.48 17.0
year_school 9 99 2.18 1.22 2.0 2.04 1.48 1.0
q85 10 99 1.64 1.32 1.0 1.32 0.00 1.0
q85_6_text* 11 99 1.03 0.22 1.0 1.00 0.00 1.0
tipi_1 12 99 3.99 1.90 4.0 3.99 2.97 1.0
tipi_2 13 99 4.15 1.53 4.0 4.23 1.48 1.0
tipi_3 14 99 5.38 1.26 6.0 5.51 1.48 1.0
tipi_4 15 99 4.29 1.69 5.0 4.31 1.48 1.0
tipi_5 16 99 5.38 1.28 6.0 5.52 1.48 1.0
tipi_6 17 99 4.76 1.64 5.0 4.84 1.48 1.0
tipi_7 18 99 5.45 1.24 6.0 5.57 1.48 2.0
tipi_8 19 99 3.17 1.70 3.0 3.09 1.48 1.0
tipi_9 20 99 5.01 1.35 5.0 5.05 1.48 2.0
tipi_10 21 99 3.10 1.48 3.0 3.04 1.48 1.0
sleep_quality 22 99 2.56 1.15 2.0 2.46 1.48 1.0
hours_of_sleep 23 99 6.51 1.04 7.0 6.63 0.00 1.0
tipi_2r 24 99 3.85 1.53 4.0 3.77 1.48 1.0
tipi_4r 25 99 3.71 1.69 3.0 3.69 1.48 1.0
tipi_6r 26 99 3.24 1.64 3.0 3.16 1.48 1.0
tipi_8r 27 99 4.83 1.70 5.0 4.91 1.48 1.0
tipi_10r 28 99 4.90 1.48 5.0 4.96 1.48 1.0
extra 29 99 3.62 1.60 3.5 3.56 2.22 1.0
agree 30 99 4.65 1.08 4.5 4.63 0.74 2.0
consc 31 99 5.11 1.22 5.5 5.15 1.48 2.0
emo 32 99 4.36 1.29 4.5 4.37 1.48 1.5
open 33 99 5.14 1.04 5.0 5.19 0.74 2.5
max range skew kurtosis se
id 1112 106.0 0.03 -1.21 3.12
progress 100 0.0 NaN NaN 0.00
duration_in_seconds 252521 251898.0 6.57 42.24 3508.05
consent 1 0.0 NaN NaN 0.00
genderid 7 6.0 -0.81 5.57 0.08
genderid_7_text* 3 2.0 7.70 61.15 0.02
sex 2 1.0 -0.02 -2.02 0.05
age 31 14.0 2.67 12.52 0.19
year_school 5 4.0 0.73 -0.44 0.12
q85 7 6.0 2.18 4.14 0.13
q85_6_text* 3 2.0 7.70 61.15 0.02
tipi_1 7 6.0 0.01 -1.34 0.19
tipi_2 7 6.0 -0.46 -0.58 0.15
tipi_3 7 6.0 -0.86 0.58 0.13
tipi_4 7 6.0 -0.17 -0.95 0.17
tipi_5 7 6.0 -0.94 0.86 0.13
tipi_6 7 6.0 -0.46 -0.86 0.17
tipi_7 7 5.0 -0.65 -0.08 0.12
tipi_8 7 6.0 0.37 -1.12 0.17
tipi_9 7 5.0 -0.29 -0.81 0.14
tipi_10 7 6.0 0.35 -0.71 0.15
sleep_quality 5 4.0 0.87 0.14 0.12
hours_of_sleep 8 7.0 -2.01 5.99 0.10
tipi_2r 7 6.0 0.46 -0.58 0.15
tipi_4r 7 6.0 0.17 -0.95 0.17
tipi_6r 7 6.0 0.46 -0.86 0.17
tipi_8r 7 6.0 -0.37 -1.12 0.17
tipi_10r 7 6.0 -0.35 -0.71 0.15
extra 7 6.0 0.18 -0.98 0.16
agree 7 5.0 0.11 0.04 0.11
consc 7 5.0 -0.32 -0.70 0.12
emo 7 5.5 -0.10 -0.54 0.13
open 7 4.5 -0.48 0.13 0.10 vars n mean sd median trimmed mad min
id 1 99 1058.12 31.05 1059.0 1057.93 38.55 1006.0
progress 2 99 100.00 0.00 100.0 100.00 0.00 100.0
duration_in_seconds 3 99 7197.29 34904.64 1461.0 1527.88 486.29 623.0
consent 4 99 1.00 0.00 1.0 1.00 0.00 1.0
genderid 5 99 4.46 0.82 4.0 4.47 1.48 1.0
genderid_7_text* 6 99 1.03 0.22 1.0 1.00 0.00 1.0
sex 7 99 1.51 0.50 2.0 1.51 0.00 1.0
age 8 99 19.78 1.84 20.0 19.53 1.48 17.0
year_school 9 99 2.18 1.22 2.0 2.04 1.48 1.0
q85 10 99 1.64 1.32 1.0 1.32 0.00 1.0
q85_6_text* 11 99 1.03 0.22 1.0 1.00 0.00 1.0
tipi_1 12 99 3.99 1.90 4.0 3.99 2.97 1.0
tipi_2 13 99 4.15 1.53 4.0 4.23 1.48 1.0
tipi_3 14 99 5.38 1.26 6.0 5.51 1.48 1.0
tipi_4 15 99 4.29 1.69 5.0 4.31 1.48 1.0
tipi_5 16 99 5.38 1.28 6.0 5.52 1.48 1.0
tipi_6 17 99 4.76 1.64 5.0 4.84 1.48 1.0
tipi_7 18 99 5.45 1.24 6.0 5.57 1.48 2.0
tipi_8 19 99 3.17 1.70 3.0 3.09 1.48 1.0
tipi_9 20 99 5.01 1.35 5.0 5.05 1.48 2.0
tipi_10 21 99 3.10 1.48 3.0 3.04 1.48 1.0
sleep_quality 22 99 2.56 1.15 2.0 2.46 1.48 1.0
hours_of_sleep 23 99 6.51 1.04 7.0 6.63 0.00 1.0
tipi_2r 24 99 3.85 1.53 4.0 3.77 1.48 1.0
tipi_4r 25 99 3.71 1.69 3.0 3.69 1.48 1.0
tipi_6r 26 99 3.24 1.64 3.0 3.16 1.48 1.0
tipi_8r 27 99 4.83 1.70 5.0 4.91 1.48 1.0
tipi_10r 28 99 4.90 1.48 5.0 4.96 1.48 1.0
extra 29 99 3.62 1.60 3.5 3.56 2.22 1.0
agree 30 99 4.65 1.08 4.5 4.63 0.74 2.0
consc 31 99 5.11 1.22 5.5 5.15 1.48 2.0
emo 32 99 4.36 1.29 4.5 4.37 1.48 1.5
open 33 99 5.14 1.04 5.0 5.19 0.74 2.5
max range skew kurtosis se
id 1112 106.0 0.03 -1.21 3.12
progress 100 0.0 NaN NaN 0.00
duration_in_seconds 252521 251898.0 6.57 42.24 3508.05
consent 1 0.0 NaN NaN 0.00
genderid 7 6.0 -0.81 5.57 0.08
genderid_7_text* 3 2.0 7.70 61.15 0.02
sex 2 1.0 -0.02 -2.02 0.05
age 31 14.0 2.67 12.52 0.19
year_school 5 4.0 0.73 -0.44 0.12
q85 7 6.0 2.18 4.14 0.13
q85_6_text* 3 2.0 7.70 61.15 0.02
tipi_1 7 6.0 0.01 -1.34 0.19
tipi_2 7 6.0 -0.46 -0.58 0.15
tipi_3 7 6.0 -0.86 0.58 0.13
tipi_4 7 6.0 -0.17 -0.95 0.17
tipi_5 7 6.0 -0.94 0.86 0.13
tipi_6 7 6.0 -0.46 -0.86 0.17
tipi_7 7 5.0 -0.65 -0.08 0.12
tipi_8 7 6.0 0.37 -1.12 0.17
tipi_9 7 5.0 -0.29 -0.81 0.14
tipi_10 7 6.0 0.35 -0.71 0.15
sleep_quality 5 4.0 0.87 0.14 0.12
hours_of_sleep 8 7.0 -2.01 5.99 0.10
tipi_2r 7 6.0 0.46 -0.58 0.15
tipi_4r 7 6.0 0.17 -0.95 0.17
tipi_6r 7 6.0 0.46 -0.86 0.17
tipi_8r 7 6.0 -0.37 -1.12 0.17
tipi_10r 7 6.0 -0.35 -0.71 0.15
extra 7 6.0 0.18 -0.98 0.16
agree 7 5.0 0.11 0.04 0.11
consc 7 5.0 -0.32 -0.70 0.12
emo 7 5.5 -0.10 -0.54 0.13
open 7 4.5 -0.48 0.13 0.10NOTE: Some variables are not numeric and are categorical variables of type character. By default, the describe() function forces non-numeric variables to be numeric and attempts to calculate descriptives for them. These variables are marked with an asterisk (*). In this case, it doesn’t make sense to calculate descriptive statistics for these variables, so we get a warning message and a bunch of NaN’s and NA’s for these variables.
A better approach would be to remove non-numeric variables before you attempt to run numerical calculations on your dataset.
Make it Pretty
Using sjPlot (https://strengejacke.github.io/sjPlot/index.html) we can make things a little more publishable! You can use select() to also keep particular variables (maybe you don’t care about the skew)
| vars | n | mean | sd | median | trimmed | mad | min | max | range | skew | kurtosis | se |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 99 | 1058.12 | 31.05 | 1059.00 | 1057.93 | 38.55 | 1006.00 | 1112 | 106.00 | 0.03 | -1.21 | 3.12 |
| 2 | 99 | 100.00 | 0.00 | 100.00 | 100.00 | 0.00 | 100.00 | 100 | 0.00 | NaN | NaN | 0.00 |
| 3 | 99 | 7197.29 | 34904.64 | 1461.00 | 1527.88 | 486.29 | 623.00 | 252521 | 251898.00 | 6.57 | 42.24 | 3508.05 |
| 4 | 99 | 1.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 1 | 0.00 | NaN | NaN | 0.00 |
| 5 | 99 | 4.46 | 0.82 | 4.00 | 4.47 | 1.48 | 1.00 | 7 | 6.00 | -0.81 | 5.57 | 0.08 |
| 6 | 99 | 1.03 | 0.22 | 1.00 | 1.00 | 0.00 | 1.00 | 3 | 2.00 | 7.70 | 61.15 | 0.02 |
| 7 | 99 | 1.51 | 0.50 | 2.00 | 1.51 | 0.00 | 1.00 | 2 | 1.00 | -0.02 | -2.02 | 0.05 |
| 8 | 99 | 19.78 | 1.84 | 20.00 | 19.53 | 1.48 | 17.00 | 31 | 14.00 | 2.67 | 12.52 | 0.19 |
| 9 | 99 | 2.18 | 1.22 | 2.00 | 2.04 | 1.48 | 1.00 | 5 | 4.00 | 0.73 | -0.44 | 0.12 |
| 10 | 99 | 1.64 | 1.32 | 1.00 | 1.32 | 0.00 | 1.00 | 7 | 6.00 | 2.18 | 4.14 | 0.13 |
| 11 | 99 | 1.03 | 0.22 | 1.00 | 1.00 | 0.00 | 1.00 | 3 | 2.00 | 7.70 | 61.15 | 0.02 |
| 12 | 99 | 3.99 | 1.90 | 4.00 | 3.99 | 2.97 | 1.00 | 7 | 6.00 | 0.01 | -1.34 | 0.19 |
| 13 | 99 | 4.15 | 1.53 | 4.00 | 4.23 | 1.48 | 1.00 | 7 | 6.00 | -0.46 | -0.58 | 0.15 |
| 14 | 99 | 5.38 | 1.26 | 6.00 | 5.51 | 1.48 | 1.00 | 7 | 6.00 | -0.86 | 0.58 | 0.13 |
| 15 | 99 | 4.29 | 1.69 | 5.00 | 4.31 | 1.48 | 1.00 | 7 | 6.00 | -0.17 | -0.95 | 0.17 |
| 16 | 99 | 5.38 | 1.28 | 6.00 | 5.52 | 1.48 | 1.00 | 7 | 6.00 | -0.94 | 0.86 | 0.13 |
| 17 | 99 | 4.76 | 1.64 | 5.00 | 4.84 | 1.48 | 1.00 | 7 | 6.00 | -0.46 | -0.86 | 0.17 |
| 18 | 99 | 5.45 | 1.24 | 6.00 | 5.57 | 1.48 | 2.00 | 7 | 5.00 | -0.65 | -0.08 | 0.12 |
| 19 | 99 | 3.17 | 1.70 | 3.00 | 3.09 | 1.48 | 1.00 | 7 | 6.00 | 0.37 | -1.12 | 0.17 |
| 20 | 99 | 5.01 | 1.35 | 5.00 | 5.05 | 1.48 | 2.00 | 7 | 5.00 | -0.29 | -0.81 | 0.14 |
| 21 | 99 | 3.10 | 1.48 | 3.00 | 3.04 | 1.48 | 1.00 | 7 | 6.00 | 0.35 | -0.71 | 0.15 |
| 22 | 99 | 2.56 | 1.15 | 2.00 | 2.46 | 1.48 | 1.00 | 5 | 4.00 | 0.87 | 0.14 | 0.12 |
| 23 | 99 | 6.51 | 1.04 | 7.00 | 6.63 | 0.00 | 1.00 | 8 | 7.00 | -2.01 | 5.99 | 0.10 |
| 24 | 99 | 3.85 | 1.53 | 4.00 | 3.77 | 1.48 | 1.00 | 7 | 6.00 | 0.46 | -0.58 | 0.15 |
| 25 | 99 | 3.71 | 1.69 | 3.00 | 3.69 | 1.48 | 1.00 | 7 | 6.00 | 0.17 | -0.95 | 0.17 |
| 26 | 99 | 3.24 | 1.64 | 3.00 | 3.16 | 1.48 | 1.00 | 7 | 6.00 | 0.46 | -0.86 | 0.17 |
| 27 | 99 | 4.83 | 1.70 | 5.00 | 4.91 | 1.48 | 1.00 | 7 | 6.00 | -0.37 | -1.12 | 0.17 |
| 28 | 99 | 4.90 | 1.48 | 5.00 | 4.96 | 1.48 | 1.00 | 7 | 6.00 | -0.35 | -0.71 | 0.15 |
| 29 | 99 | 3.62 | 1.60 | 3.50 | 3.56 | 2.22 | 1.00 | 7 | 6.00 | 0.18 | -0.98 | 0.16 |
| 30 | 99 | 4.65 | 1.08 | 4.50 | 4.63 | 0.74 | 2.00 | 7 | 5.00 | 0.11 | 0.04 | 0.11 |
| 31 | 99 | 5.11 | 1.22 | 5.50 | 5.15 | 1.48 | 2.00 | 7 | 5.00 | -0.32 | -0.70 | 0.12 |
| 32 | 99 | 4.36 | 1.29 | 4.50 | 4.37 | 1.48 | 1.50 | 7 | 5.50 | -0.10 | -0.54 | 0.13 |
| 33 | 99 | 5.14 | 1.04 | 5.00 | 5.19 | 0.74 | 2.50 | 7 | 4.50 | -0.48 | 0.13 | 0.10 |
ggplot2
ggplot2 from the tidyverse
Since we have already installed and loaded the library, we don’t have to do anything else at this point!
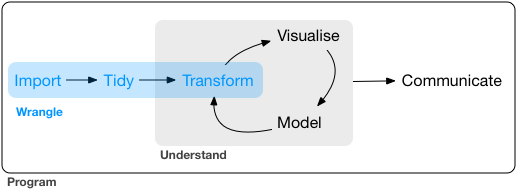
ggplot2 follows the “grammar of graphics”
- Theoretical framework for creating data visualizations
- Breaks the process down into separate components:
Data
Aesthetics (aes)
Geometric Objects (geoms)
Faceting
Themes
Grammar of Graphics
ggplot2 cheatsheet
ggplot2 syntax
There is a basic structure to create a plot within ggplot2, and consists of at least these three things:
- A Data Set
- Coordinate System
- Geoms - visual marks to represent the data points
In R it looks like this:
ggplot2 syntax
Let’s start with a basic figure with our TIPI data
First we will define the data that we are using and the variables we are visualizing
What happens?
We forgot to tell it what to do with the data!

Need to add the appropriate geom to have it plot points for each observation
Note: the geom_point() layer will “inherit” what is in the aes() in the previous layer
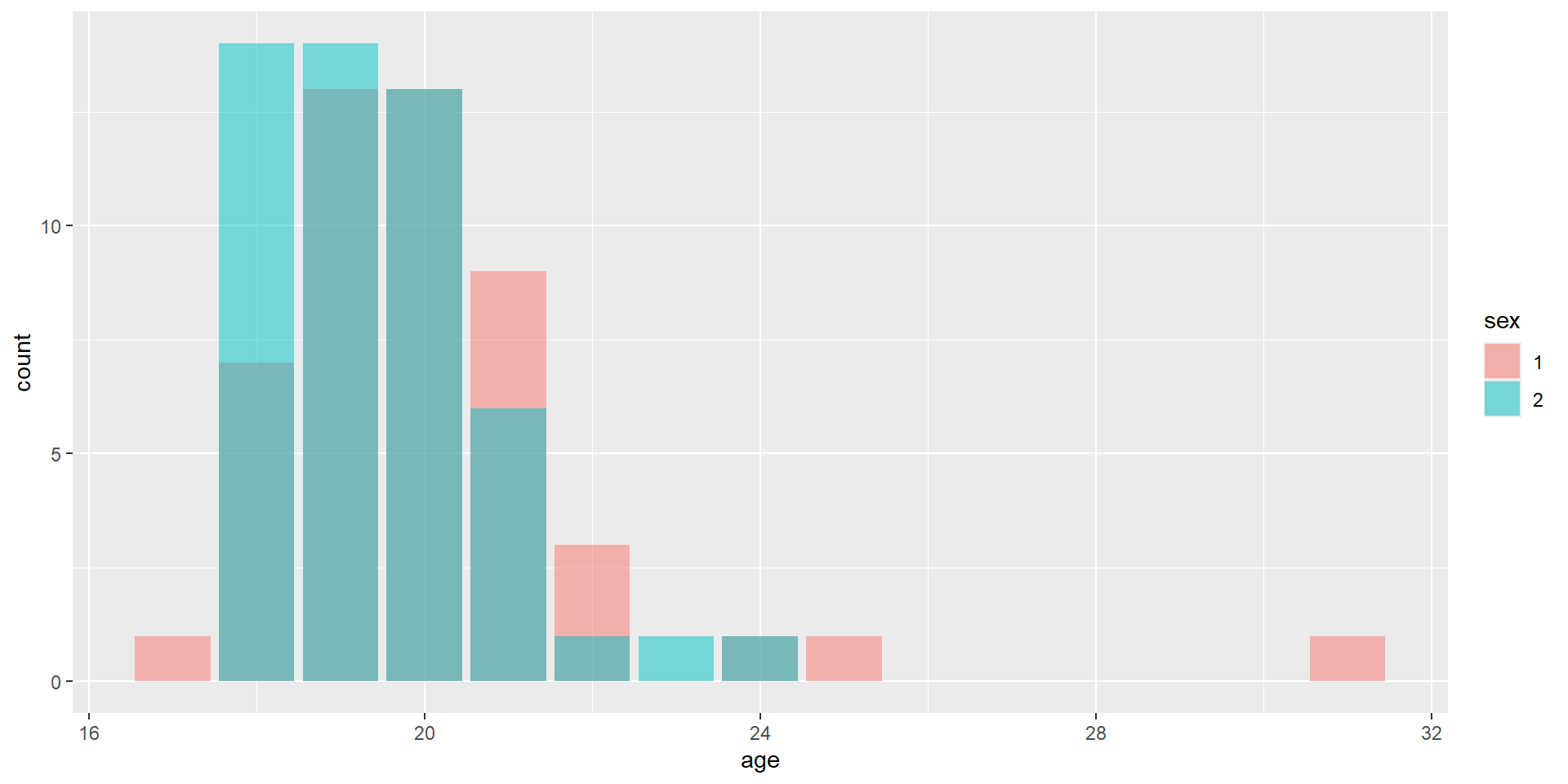
Adding in Color
Maybe we would like to have each of the points colored by their respective sex
This information will be added to the aes() within the geom_point() layer
Including a fit line
Why don’t we put in a line that represents the relationship between these variables?
We will want to add another layer/geom
That looks a little wonky…why is that? Did you get a note in the console?
Including a fit line
The geom_smooth() defaults to using a loess line to fit to the data
In order to update that, we need to change some of the defaults for that layer and specify that we want a “linear model” or lm function to the data
Did that look a little better?
Individual fit lines
It might make more sense to have individual lines for each of the species instead of something that is across all
What did we move around from the last set of code?
What was the error you got?
Data Types
It looks like R is looking at our binary variable as a continuous number
We want to be able to tell our code that these are categories/factors
If we want to change or compute a new variable, what do we use?
Let’s try that again:
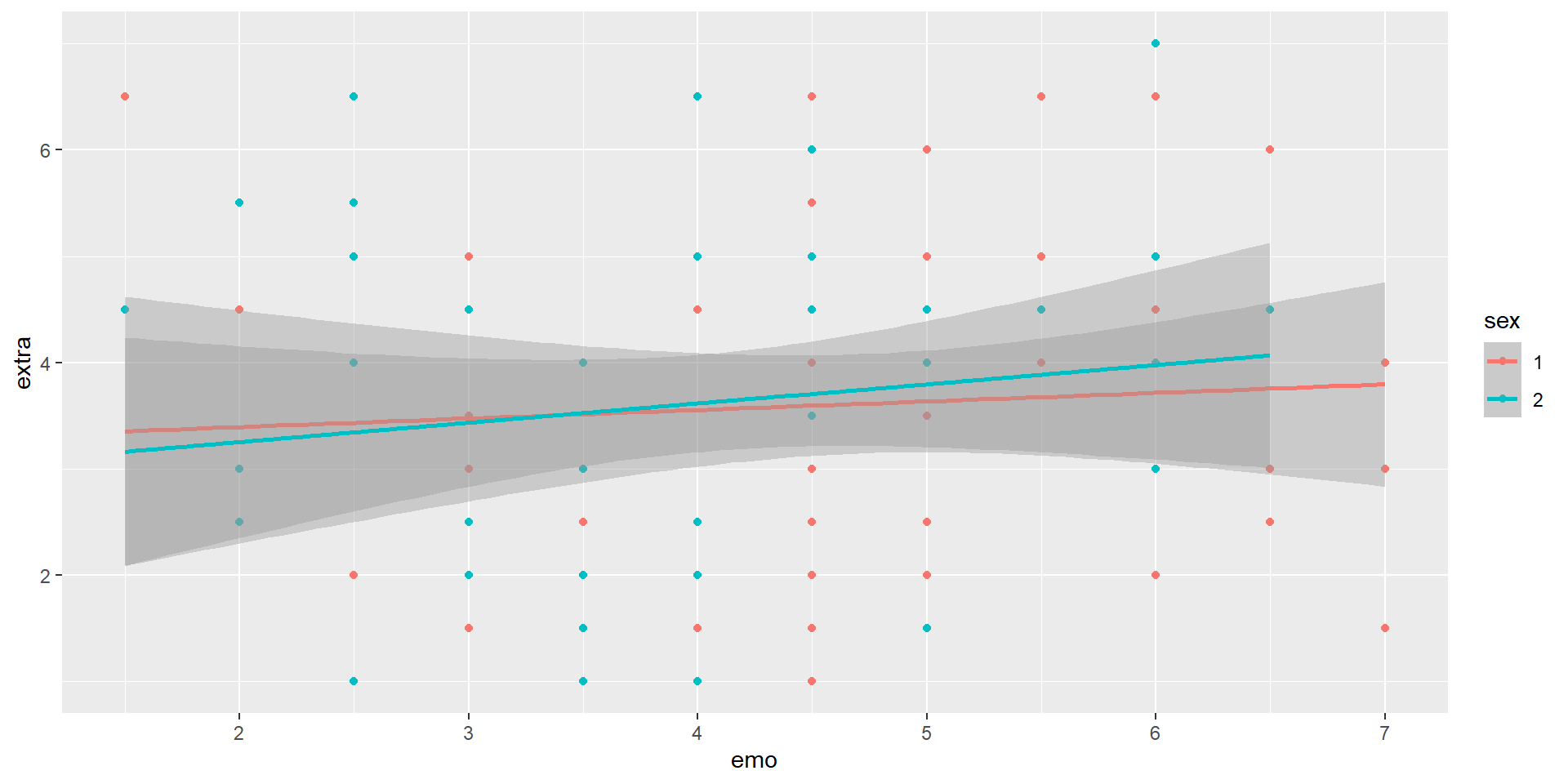
Updating Labels/Title
It will default to including the variable names as the x and y labels, but that isn’t something that makes sense. Also would be good to have a title!
We add on another layer called labs() for our labels (link)
Other Graphs
Take another look at the ggplot cheatsheet
What else is a useful chart?