Week 09: Model Selection & Variability

Date: October 19, 2025

Today…

Regression & Model Selection

#Don't know if I'm using all of these, but including theme here anyways
library(tidyverse)
library(rio)
library(broom)
library(psych)
library(here)


#Remove Scientific Notation 
options(scipen=999)

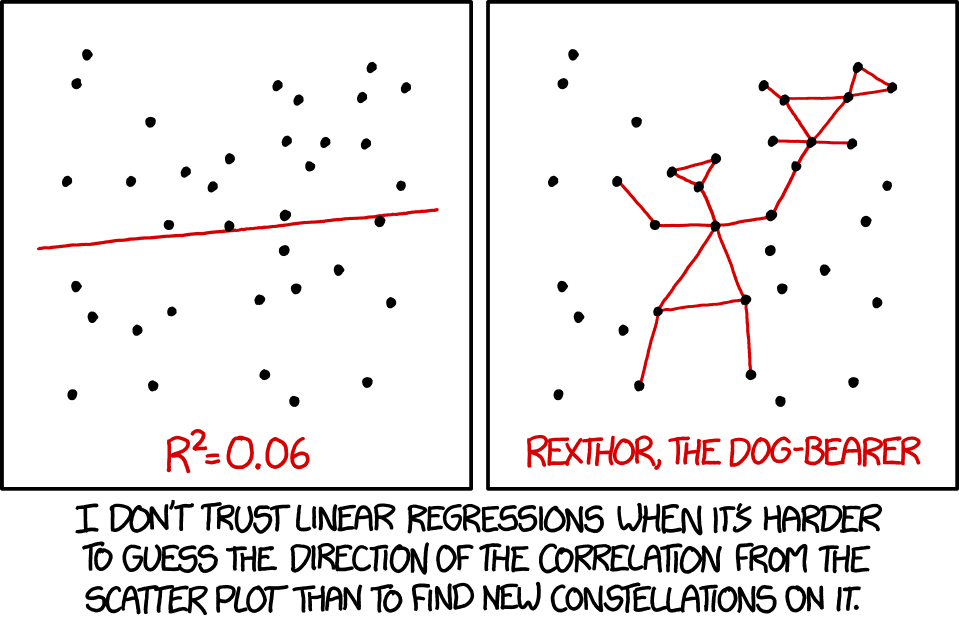
Regressions

With regression, we are building a model that we think best represents the data, and the broader world

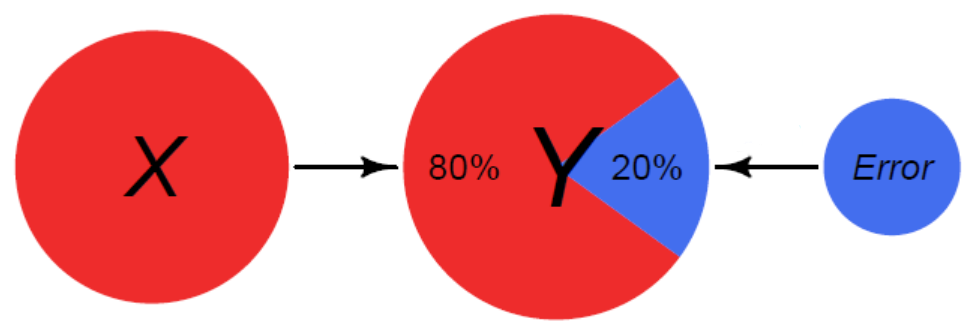
\[ Data = Model + error \]

Regression Equation

Overall, we are providing a model to give us a “best guess” on predicting our outcome

\[ Y_i = b_0 + b_1X_i + e_i \]

This equation is capturing how we are able to calculate each observation ( \(Y_i\) )

Term Meaning
\(b_0\) Intercept - when X = 0
\(b_1\) Slope - for every 1 unit change in X, there are \(b_1\) unit change in Y
\(X_i\) Predictor Variable
\(e_i\) Error/Residuals

Unstandardized vs. Standardized

What is the Difference? (other than the runes)

Unstandardized:

\[ Y_i = b_0 + b_1X_i + e_i \]

Standardized:

\[ Y_i = \beta_0 + \beta_1X_i + \epsilon_i \]

\[ Z_y = \beta_0 + \beta_1Z_x + \epsilon_i \]

Example - LEGO Data

lego <- import(here("files", "data", "LEGO_data.csv")) %>% 
  janitor::clean_names()

describe(lego)
                 vars  n     mean       sd   median  trimmed      mad      min
set_name*           1 59    30.00    17.18    30.00    30.00    22.24     1.00
set_number          2 59 37023.29 25089.50 31167.00 35693.88 30827.70 10294.00
number_of_pieces    3 59  2416.58  2384.39  1503.00  2073.37  1906.62   104.00
price               4 59   218.19   214.72   129.99   189.81   163.09     9.99
                      max range skew kurtosis      se
set_name*           59.00    58 0.00    -1.26    2.24
set_number       76974.00 66680 0.55    -1.21 3266.37
number_of_pieces 10001.00  9897 1.32     1.37  310.42
price              999.99   990 1.28     1.48   27.95

Visualization

Good to see the scatterplots of this relationship

lego %>% 
  ggplot(aes(number_of_pieces, price)) + 
  geom_point() + 
  geom_smooth(method = "lm")

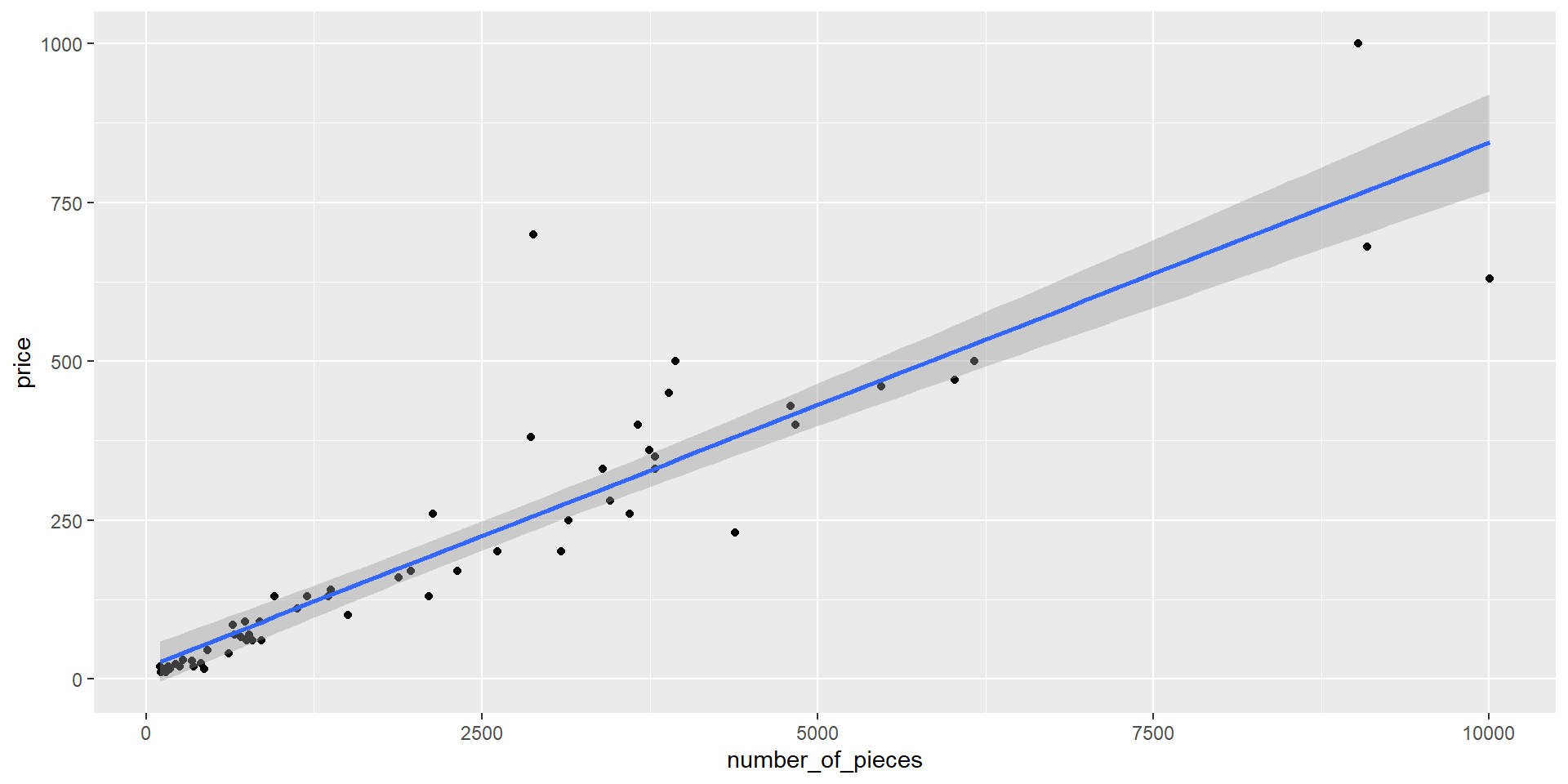
Estimating Coefficients

  • We are bringing in 2 sources of data (information we don’t need to estimate)

    • # of Pieces (Mean = 2416.5762712, SD = 2384.3877997)

    • Set Price (Mean = 218.1935593, SD = 214.7204998)

  • Need to estimate \(b_0\) and \(b_1\)

Regression coefficient, \(b_{1}\)

Calculating the slope

\[\Large b_{1} = \frac{cov_{XY}}{s_{x}^{2}}\]

# Covariance
cov(lego$number_of_pieces, lego$price)
[1] 469162.5
# Variance of # of Pieces
var(lego$number_of_pieces)
[1] 5685305

🚧 Brief Detour - Calculating (Co)Variances

Variance: The average squared difference between each data point and the mean; How far each observation is from the mean, on average, in squared units

\[ Var(X) = \frac1{N-1} \sum (X_i - \bar X)^2 \]

Covariance: Average cross product of deviations; How related are the deviations of two different variables across observations

\[ Cov(X, Y) = \frac 1{N-1} \sum (X_i - \bar{X}) (Y_i - \bar{Y}) \]

Example on the board (reminder to Dr. Haraden to do something here)

  • Note where the regression line passes through

  • Look at deviations (variance) to covariance

Code 
mprice <- mean(lego$price)
mnum <- mean(lego$number_of_pieces)

lego %>% 
  ggplot(aes(number_of_pieces, price)) + 
  geom_point() + 
  geom_hline(yintercept = mprice, 
             color = "orange", 
             linewidth = 1.5) + 
  geom_vline(xintercept = mnum, 
             color = "purple", 
             linewidth = 1.5) + 
  geom_smooth(method = "lm", se = FALSE, 
              color = "black", linewidth = 1.5)

Regression coefficient, \(b_{1}\)

\[\Large b_{1} = \frac{cov_{XY}}{s_{x}^{2}} = r_{xy} \frac{s_{y}}{s_{x}}\]

#SD of # of Pieces
sd(lego$number_of_pieces) 
[1] 2384.388
# SD of Price
sd(lego$price) 
[1] 214.7205
# Correlation
cor(lego$number_of_pieces, lego$price)
[1] 0.9163742

Regression Coefficient, \(b_0\)

Calculating the Intercept:

\[\Large b_0 = \bar{Y} - b_1\bar{X}\]

The intercept adjusts the location of the regression line to ensure that it runs through the point \(\large (\bar{X}, \bar{Y}).\)

mean(lego$number_of_pieces)
[1] 2416.576
mean(lego$price)
[1] 218.1936

What is the Regression Model?

Using the calculations, identify what the linear model would be.

What is the Regression Model?

Using the calculations, identify what the linear model would be.

You hear about 3 new sets coming out that you are interested in. Since you have this regression model, you can calculate the total price for each. How much money do you need to save (excluding taxes) to buy all 3 sets?

Set 1: 1031 pieces Set 2: 357 Set 3: 4154

Before the Break

Take the Stroop Task and record your incongruent, congruent and stroop effect on your worksheet

Back to the Show

Last time on “Stats Island”, Dr. Haraden asked everyone to look at colors and words. Plus, Rupert was voted off the island. Who could be next??

Explaining Variance

Stroop Data Modeling

Research Question: Sleep Quality is negatively related to the Stroop Effect. Lower sleep quality will predict a greater Stroop effect.

Data Set (I hope I entered all the data in appropriately)

Explaining Variance

Visualize the Stroop Effect data

  • What is the best “model” to explain this data? If you had no information, what would be your best guess for someone’s score?

. . .

We are looking to explain variance in our outcome (Stroop Performance)

Note

The total distance from the mean to each point is the Total Sum of Squares - The total amount of “error” we are trying to explain

The mean can be considered the “null model” in that it is the most basic

Null to Sleep model

We can then introduce another variable to try explain more of the variance in the Stroop Effect

Note

There should be some visualizations on the board with mean and regression lines

The distance from each point down to the original ‘mean’ is the total deviation.

The portion from the ‘mean’ up to our new ‘sleep model’ is the explained deviation (SSM). This is the improvement we gained by considering sleep!

The leftover bit from our ‘sleep model’ to the actual data point is the unexplained residual (SSE). This is the error our model couldn’t account for.

Linear Regression

Use the information and let’s do it in R instead of on the board

Visualize the relationship

Run a linear regression

Model Fit

Take a look at the \(R^2\) value

Is there any other data that we have that could impact overall Stroop Effects?

After including it in the model, we can examine the change in \(R^2\)

What would happen if we put the random number variable in there?

Comparing Models

Can compare models using an ANOVA when one model is nested within another

Note

Nested Models: where one model (Model 0) contains a subset of the predictors from the other one (Model 1). Model 1 contains all of the predictors included in Model 0, plus one or more additional predictors. When this happens we say that Model 0 is nested within Model 1.

Model Diagnostics

As we get more complex, we want to be sure to check how our model is functioning. One way is to use \(adjusted \ R^2\) to get a sense of the amount of variance each predictor is bringing.

Need to be careful of overfitting the model to the data

Multicollinearity - when predictors are highly related to one another

  • Checked with the Variance Inflation Factor (VIF)

Homogeneity of Variance - the variance of the residuals is assumed to be constant

check_models

This will check everything for you in regressions, let’s try it out

https://easystats.github.io/performance/reference/check_model.html

Selecting a Model

One of the most daunting tasks can be identifying the “right” statistical model for the data you have

You may see flowcharts like this:

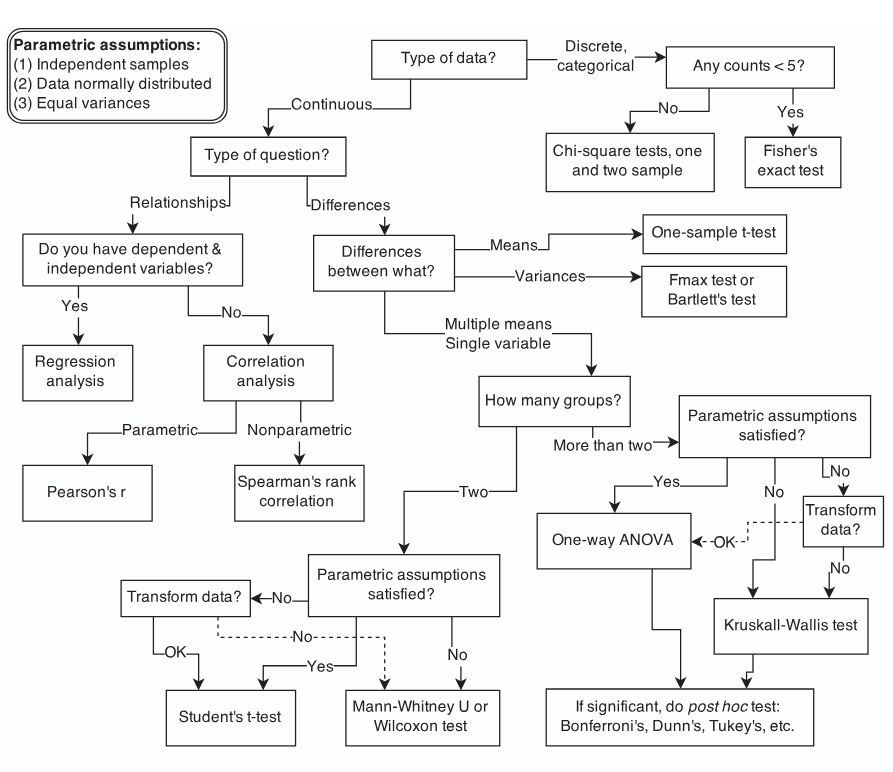
Selecting a Model

If you are asking which model is “right”, you are doing it backwards

“All models are wrong, some models are useful.” -George Box

Remember: \(Data (The\ Truth) = Model + Error\)

Instead, think about identifying a model as “Model Based Reasoning” in which you will need to defend the choices you made

Example: t-test vs. ANOVA vs. Regression

This might be something that we are considering between. How do we pick the “right” one?

Start with some data where we have 2 groups and we identify a 2 point difference in the groups scores

set.seed(2025)

# Two independent groups with equal variances
n0 <- 80; n1 <- 80
mu0 <- 12; mu1 <- 10      # true mean difference = -2
sigma <- 3
y0 <- rnorm(n0, mu0, sigma)
y1 <- rnorm(n1, mu1, sigma)

# Put that in a data frame
dat <- data.frame(
  dep = c(y0, y1),
  group01 = c(rep(0, n0), rep(1, n1))
) %>% 
  mutate(group = factor(group01, levels = c(0,1), labels = c("control","treatment")))

t-test

tt_fit <- t.test(dep ~ group, data = dat, var.equal = TRUE)
tt_tidy <- tidy(tt_fit)
tt_tidy
# A tibble: 1 × 10
  estimate estimate1 estimate2 statistic    p.value parameter conf.low conf.high
     <dbl>     <dbl>     <dbl>     <dbl>      <dbl>     <dbl>    <dbl>     <dbl>
1     2.68      12.1      9.46      5.75    4.48e-8       158     1.76      3.60
# ℹ 2 more variables: method <chr>, alternative <chr>

ANOVA

fit_aov <- aov(dep ~ group, data = dat)
summary(fit_aov)
             Df Sum Sq Mean Sq F value       Pr(>F)    
group         1  286.6  286.64   33.07 0.0000000448 ***
Residuals   158 1369.6    8.67                         
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
aov_tidy <- tidy(fit_aov)

Regression

reg_fit <- lm(dep ~ group01, data = dat)
reg_tidy <- tidy(reg_fit)
reg_tidy
# A tibble: 2 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    12.1      0.329     36.9  1.65e-79
2 group01        -2.68     0.466     -5.75 4.48e- 8
reg_glance <- glance(reg_fit)

Comparing Methods

# Equivalence 1: The regression slope for the dummy variable equals the difference in group means.
mean_diff <- tt_tidy$estimate2 - tt_tidy$estimate1
beta1 <- reg_tidy %>% 
  filter(term == "group01") %>% 
  pull(estimate)

mean_diff
[1] -2.676943
beta1
[1] -2.676943
# Equivalence 2: The F-statistic from the ANOVA is the regression square of the t-statistic.
t_stat_reg <- reg_tidy %>% 
  filter(term == "group01") %>% 
  pull(statistic)

t_stat_t <- tt_tidy %>% 
  pull(statistic)

f_stat <- reg_glance$statistic


t_stat_reg^2
[1] 33.06772
t_stat_t^2
       t 
33.06772 
f_stat
   value 
33.06772 
# Equivalence 3: The p-values are identical.
tt_tidy$p.value
[1] 0.00000004475048
reg_tidy %>% 
  filter(term == "group01") %>% 
  pull(p.value)
[1] 0.00000004475048
aov_tidy %>% 
  filter(term == "group") %>% 
  pull(p.value)
[1] 0.00000004475048

Examples in R

Try some live coding! Also known as “Another opportunity for Dr. Haraden to potentially embarrass himself”

https://archive.ics.uci.edu/dataset/320/student+performance

https://archive.ics.uci.edu/dataset/697/predict+students+dropout+and+academic+success

https://datahub.io/collections

https://www.kaggle.com/datasets