Correlation

PSYC 640 - Fall 2023

Dustin Haraden, PhD

Last Class

  • Two Way ANOVA
    • Comparing means across multiple groups/levels

Looking Ahead

  • R-Workshop! (Link to Sign up)
    • 11/3 & 12/1 from 2-3pm
  • Final Project Updates:
    • Introduction & Methods draft due 11/15 (Peer Review)
    • Data Analysis draft due 11/27 (Peer Review)

Today…

Linear Relationships - Correlation

  • Pearson Correlation

  • Spearman’s Rank Correlation

  • Missing Data

  • Creating correlation matrices

# for dplyr, ggplot2
library(tidyverse)
#Loading data
library(rio)
# nice tables/plots
library(sjPlot)
library(kableExtra)
library(ggpubr)


#Remove Scientific Notation 
options(scipen=999)

Relationships between variables (Ch 5.7)

Association - Correlation

Examine the relationship between two continuous variables

Similar to the mean and standard deviation, but it is between two variables

Typically displayed as a scatterplot

Code 
set.seed(42)

n <- 200
x <- rnorm(n, mean = 10, sd = 2)
y <- 2 * x + rnorm(n, mean = 0, sd = 2) 
corr_data <- data.frame(x,y)

corr_data %>% 
  ggplot(aes(x,y)) + 
  geom_point() + 
  geom_smooth(method="lm", 
              se = FALSE) + 
  labs(
    x = "Number of Houses", 
    y = "Amount of Candy"
  )

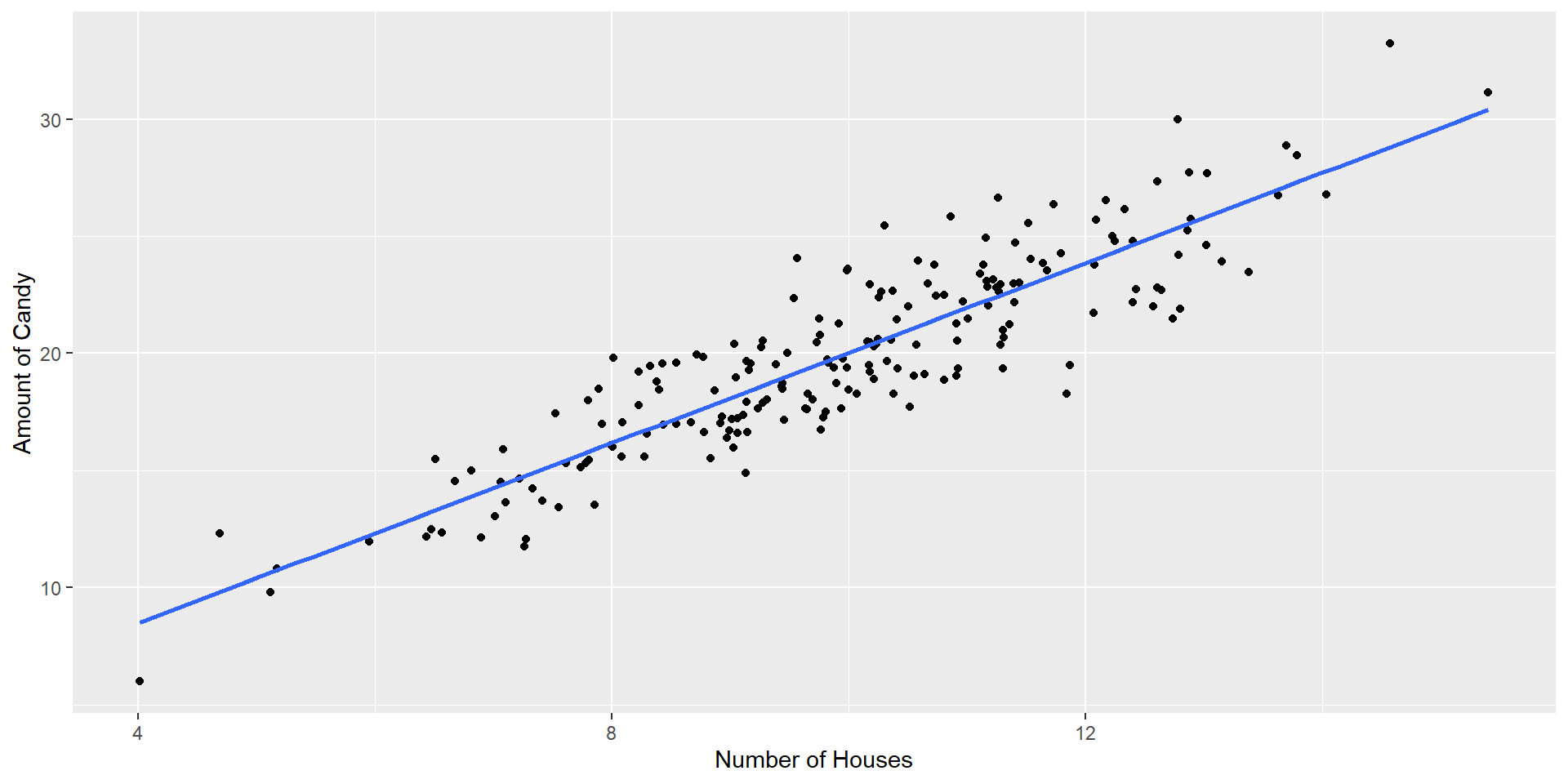
Association - Covariance

Before we talk about correlation, we need to take a look at covariance

\[ cov_{xy} = \frac{\sum(x-\bar{x})(y-\bar{y})}{N-1} \]

  • Covariance can be thought of as the “average cross product” between two variables

  • It captures the raw/unstandardized relationship between two variables

  • Covariance matrix is the basis for many statistical analyses

Covariance

Let’s take a look back at that data before and get the covariance

cov(corr_data)
         x         y
x 3.799265  7.301818
y 7.301818 17.598057

  • What does having a covariance of 7.3 actually mean though?

  • We have to interpret the covariance in terms of the units present (x = # of houses and y = amount of candy)

    • The scale is \(x*y\) … what does that even mean?

Covariance to Correlation

The Pearson correlation coefficient \(r\) addresses this by standardizing the covariance

It is done in the same way that we would create a \(z-score\)…by dividing by the standard deviation

\[ r_{xy} = \frac{Cov(x,y)}{sd_x sd_y} \]

Correlations

  • Tells us: How much 2 variables are linearly related

  • Range: -1 to +1

  • Most common and basic effect size measure

  • Is used to build the regression model

Interpreting Correlations (5.7.5)

Correlation Strength Direction
-1.0 to -0.9 Very Strong Negative
-0.9 to -0.7 Strong Negative
-0.7 to -0.4 Moderate Negative
-0.4 to -0.2 Weak Negative
-0.2 to 0 Negligible Negative
0 to 0.2 Negligible Positive
0.2 to 0.4 Weak Positive
0.4 to 0.7 Moderate Positive
0.7 to 0.9 Strong Positive
0.9 to 1.0 Very Strong Positive

Hypothesis Testing - Correlation

Statistical Test - Correlation

We tend to always compare our correlations to the null (0)

Hypotheses:

  • \(H_0: r_{xy} = 0\)

  • \(H_1:r_{xy} \neq 0\)

Assumptions:

  • Observations are independent

  • Linear Relationship

Statistical Test - Correlation

When comparing to 0, we can use the steps similar to a t-test

Calculate the test statistic (df = N - 2):

\[ t = \frac{r}{\sqrt{\frac{1-r^2}{N-2}}} \]

Then follow the typical steps for a t-test!

Statistical Test - But not always

It isn’t always that easy though…

We were able to use the \(t-distribution\) previously because we assumed the null was 0. However, we cannot do that when:

  • The null \(\neq\) 0

  • Calculating Confidence Intervals for correlations

  • Comparing two correlations against each other

Will need to transform the \(r\) to a \(z\) using Fisher’s r to z’ transformation (beyond this class)

\[ z' = \frac{1}{2}ln\frac{1+r}{1-r} \]

Pearson Correlations in R

Calculating Correlation in R

Now how do we get a correlation value in R?

cor(corr_data$x, corr_data$y)
[1] 0.8929946

That will give us the correlation, but we also want to know how to get our p-value

Correlation Test

To get the test of a single pair of variables, we will use the cor.test() function:

cor.test(x, y, data = corr_data)

    Pearson's product-moment correlation

data:  x and y
t = 27.919, df = 198, p-value < 0.00000000000000022
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.8609168 0.9180000
sample estimates:
      cor 
0.8929946

Using real data - NY & NM

So far we have been looking at single variables, but we often care about the relationships between multiple variables in a dataset

Code 
school <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/NM-NY_CAS.csv") %>% 
  select(Ageyears, Sleep_Hours_Schoolnight, Sleep_Hours_Non_Schoolnight,
         Reaction_time, Score_in_memory_game) %>% 
  janitor::clean_names()

cor(school) %>% 
  kable()
ageyears sleep_hours_schoolnight sleep_hours_non_schoolnight reaction_time score_in_memory_game
ageyears 1 NA NA NA NA
sleep_hours_schoolnight NA 1 NA NA NA
sleep_hours_non_schoolnight NA NA 1 NA NA
reaction_time NA NA NA 1 NA
score_in_memory_game NA NA NA NA 1

Missing Values

Handling Missing - Correlation

  • Listwise Deletion (complete cases)

    • Removes participants completely if they are missing a value being compared
    • Smaller Sample Sizes
    • Doesn’t bias correlation estimate

  • Pairwise Deletion

    • Removes participants for that single pair, but leaves information in when there are complete information
    • Larger Sample Sizes
    • Could bias estimates if there is a systematic reason things are missing
cor(school, use = "complete") %>% kable()
ageyears sleep_hours_schoolnight sleep_hours_non_schoolnight reaction_time score_in_memory_game
ageyears 1.0000000 -0.3771818 0.0259458 0.0582001 -0.1140799
sleep_hours_schoolnight -0.3771818 1.0000000 0.0563271 0.0549937 0.0533009
sleep_hours_non_schoolnight 0.0259458 0.0563271 1.0000000 -0.0908150 0.0726865
reaction_time 0.0582001 0.0549937 -0.0908150 1.0000000 -0.0069244
score_in_memory_game -0.1140799 0.0533009 0.0726865 -0.0069244 1.0000000 
cor(school, use = "pairwise") %>% kable()
ageyears sleep_hours_schoolnight sleep_hours_non_schoolnight reaction_time score_in_memory_game
ageyears 1.0000000 -0.3756825 0.0203699 0.0525420 -0.0531333
sleep_hours_schoolnight -0.3756825 1.0000000 0.0593331 0.0548024 0.0532172
sleep_hours_non_schoolnight 0.0203699 0.0593331 1.0000000 -0.0894077 0.0726865
reaction_time 0.0525420 0.0548024 -0.0894077 1.0000000 -0.0069010
score_in_memory_game -0.0531333 0.0532172 0.0726865 -0.0069010 1.0000000

Spearman’s Rank Correaltion

Shortcomings of Pearson Correlation

Focus on linear relationships - how data fall on a single straight line

  • We assume that with any increase in our X variable, there is an equal amount of increase in Y across the whole variable
  • Example: relation between studying/effort and grade
    • If you put 0 effort you would expect a 0 grade
    • However, a little bit of effort might be related to a grade of 45
    • But more effort will need to take place in order to go from 45 - 90 than it does to go from 0 - 45

Spearman’s Rank Correlation

We need to be able to capture this different (ordinal) “relationship”

  • If student 1 works more hours than student 2, then we can guarantee that student 1 will get a better grade

Instead of using the amount given by the variables (“hours studied”), we rank the variables based on least (rank = 1) to most (rank = 10)

Then we correlate the rankings with one another

Foundations of Statistics

Who were those white dudes that started this?

Statistics and Eugenics

The concept of the correlation is primarily attributed to Sir Frances Galton

The correlation coefficient was developed by his student, Karl Pearson, and adapted into the ANOVA framework by Sir Ronald Fisher

  • Both were prominent advocates for the eugenics movement

What do we do with this info?

Be aware of the assumptions

  • Statistics are often thought of as being absent of bias…they are just numbers

  • Statistical significance was a way to avoid talking about nuance or degree.

  • “Correlation does not imply causation” was a refutation of work demonstrating associations between environment and poverty.

  • Need to be particularly mindful of our goals as scientists and how they can influence the way we interpret the findings

Fancy Tables

Correlation Tables

Before we used the cor() function to create a correlation matrix of our variables

But what is missing?

cor(school, use = "complete") %>% 
  kable()
ageyears sleep_hours_schoolnight sleep_hours_non_schoolnight reaction_time score_in_memory_game
ageyears 1.0000000 -0.3771818 0.0259458 0.0582001 -0.1140799
sleep_hours_schoolnight -0.3771818 1.0000000 0.0563271 0.0549937 0.0533009
sleep_hours_non_schoolnight 0.0259458 0.0563271 1.0000000 -0.0908150 0.0726865
reaction_time 0.0582001 0.0549937 -0.0908150 1.0000000 -0.0069244
score_in_memory_game -0.1140799 0.0533009 0.0726865 -0.0069244 1.0000000

Correlation Tables - sjPlot

tab_corr(school, na.deletion = "listwise", triangle = "lower")
  ageyears sleep_hours_schoolnight sleep_hours_non_schoolnight reaction_time score_in_memory_game
ageyears          
sleep_hours_schoolnight -0.377***        
sleep_hours_non_schoolnight 0.026 0.056      
reaction_time 0.058 0.055 -0.091    
score_in_memory_game -0.114 0.053 0.073 -0.007  
Computed correlation used pearson-method with listwise-deletion.

Correlation Tables - sjPlot

So many different cusomizations for this type of plot

Can add titles, indicate what missingness and method

Saves you a TON of time when putting it into a manuscript

Visualizing Data

Visualizing Data

It is always important to visualize our data! Even after getting the correlations and other descriptives

Let’s go back to the data that we had in a previous lecture

Code 
data1 <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/data1.csv") %>% 
  mutate(dataset = "data1")

data2 <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/data2.csv") %>% 
  mutate(dataset = "data2")

data3 <- import("https://raw.githubusercontent.com/dharaden/dharaden.github.io/main/data/data3.csv") %>% 
  mutate(dataset = "data3")

And then combine them to make it easier

three_data <- bind_rows(data1, data2, data3)

Descriptive Stats on the 3 datasets

three_data %>%
  group_by(dataset) %>% 
  summarize(
    mean_x = mean(x),
    mean_y = mean(y),
    std_x = sd(x), 
    std_y = sd(y), 
    cor_xy = cor(x,y)
  )
# A tibble: 3 × 6
  dataset mean_x mean_y std_x std_y  cor_xy
  <chr>    <dbl>  <dbl> <dbl> <dbl>   <dbl>
1 data1     54.3   47.8  16.8  26.9 -0.0641
2 data2     54.3   47.8  16.8  26.9 -0.0683
3 data3     54.3   47.8  16.8  26.9 -0.0645

Visualizing Dataset 1

Code 
data1 %>% 
  ggplot(aes(x, y)) + 
  geom_point() + 
  labs(title = "Dataset 1")

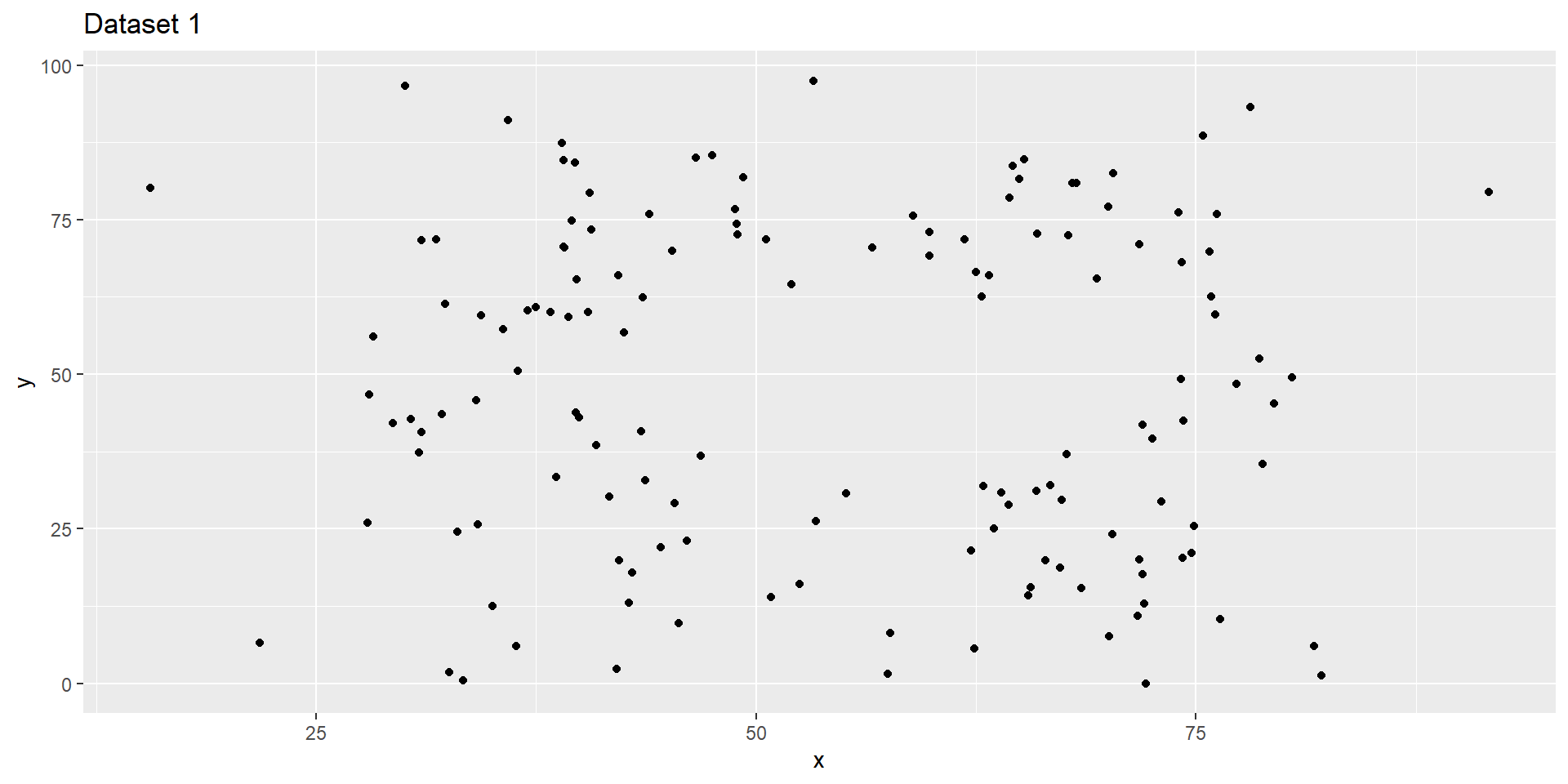
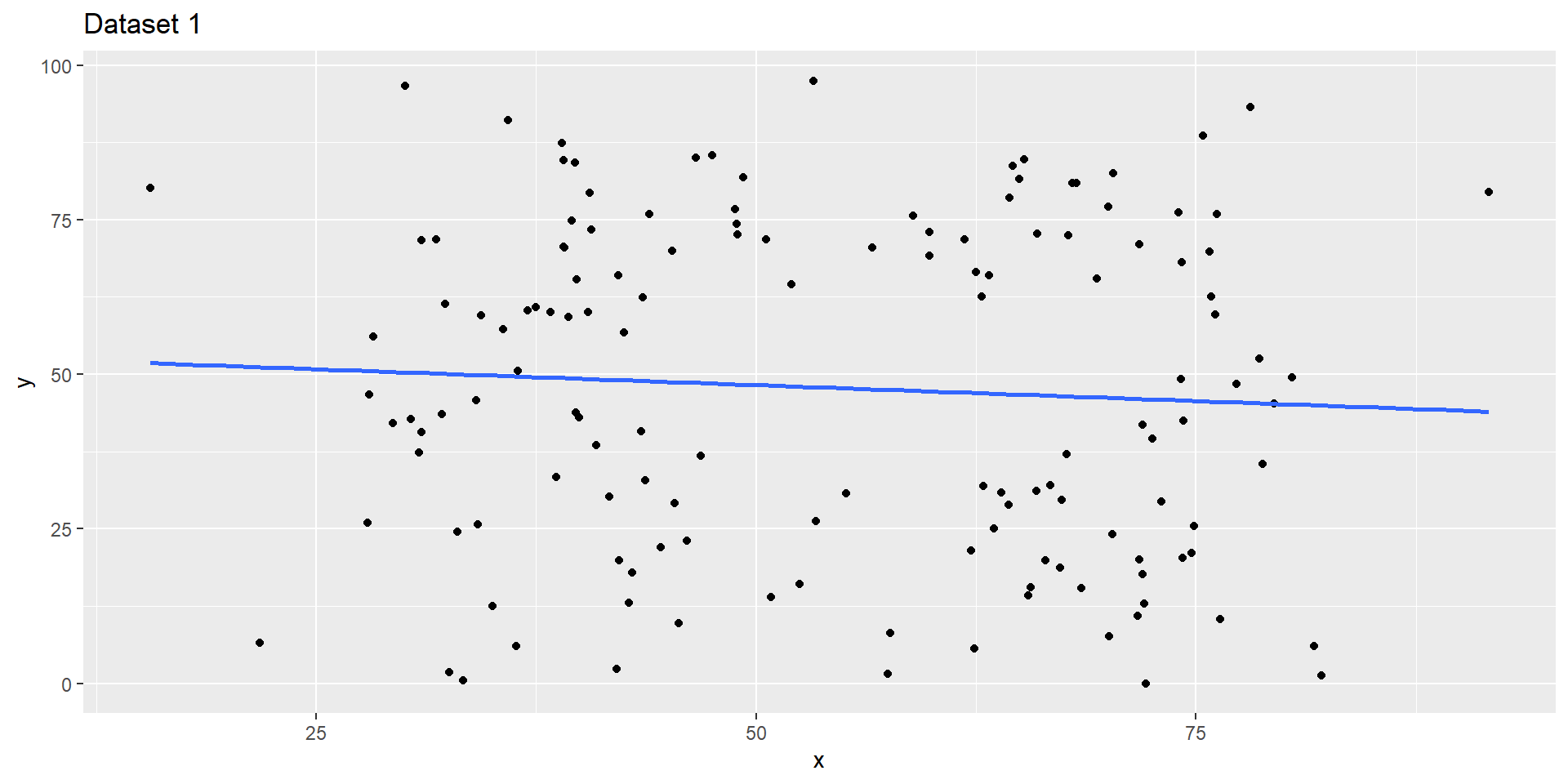
Visualizing Dataset 1

Code 
data1 %>% 
  ggplot(aes(x, y)) + 
  geom_point() + 
  labs(title = "Dataset 1") +
  geom_smooth(method = "lm", 
              se = FALSE)

Visualizing Dataset 1

data1 %>% 
  ggscatter("x", "y", 
            add = "reg.line") + 
  stat_cor(label.y = 55) + 
  labs(title = "Dataset 1")

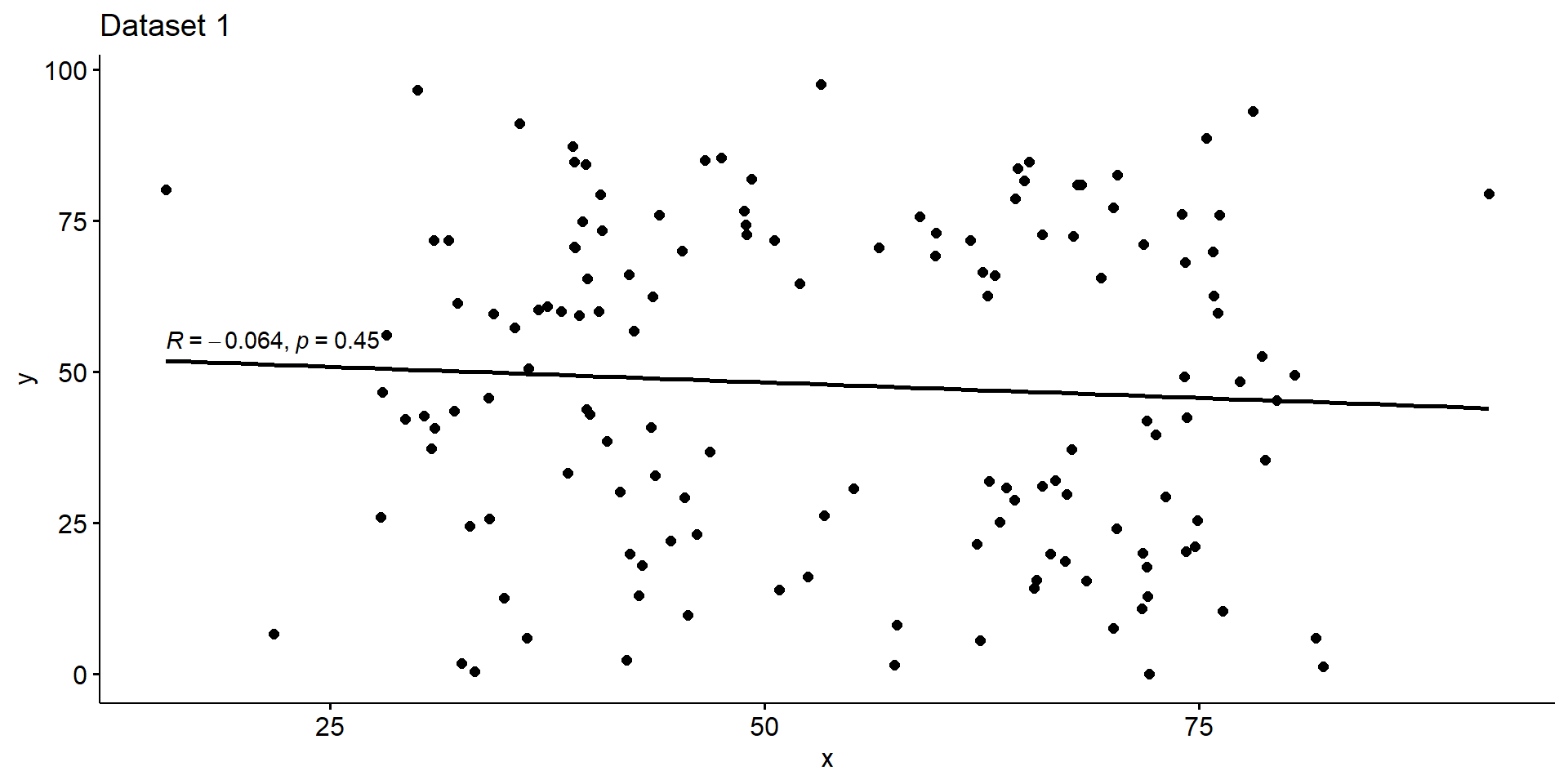
Visualizing Dataset 2

Let’s try it out in R!

Next time…

  • More Correlation?
  • Maybe Regression? (Y = mX + b)
  • Group Work!